Diese Seite ist der "Renner"!
Jeden Monat werden derzeit etwa 2400 Seiten bei mir aufgerufen (in den Schulferien weniger). Regelmäßig mit etwa 200 Aufrufen ist diese Seite der "Renner". Mich interessiert sehr, warum das so ist und wie Sie auf diese Seite aufmerksam (gemacht) wurden. Vielleicht mag die Eine oder der Andere mir das mal schreiben? Ich freue mich sehr auf Post!
55 dB Hörverlust - was heißt das, was und wie hört man dann?
Einige Erläuterungen zu Schallpegeln, Lautstärke und zum Rechnen mit dB
Sowohl Schallpegel (umgangssprachlich auch Lautstärke genannt) als auch Hörverluste werden in dB angeben. Kaum jemand traut sich nachzufragen, was das denn überhaupt bedeutet und wenn tatsächlich eine solche Frage gestellt wird, dann erhält man häufig von verschiedenen Personen unterschiedliche Aussagen, z. B. ein bestimmter dB-Wert sei halb oder doppelt so viel, 10, 100 oder 1000-mal mehr und andere sagen wieder halb oder doppelt so laut. Dabei gehen die (jeweils teilweise richtigen) Aussagen bunt durcheinander und hinterher wundert man sich, dass irgend-jemand überhaupt noch etwas Richtiges weiß. Der folgende Beitrag will versuchen, mit nur ganz wenig Mathematik einige grundlegende Kenntnisse zu vermitteln.
Schallpegel und Hörverluste werden in dB (dezi-Bel) angegeben und das ist „dummerweise“ ein logarithmisches Maß. Das Wort „dummerweise“ ist deshalb in Ausführungszeichen gesetzt, weil es nach dem so genannten Weber-Fechnerschen Gesetz richtig und zwangsläufig ist [1] [2]. Der Mensch empfindet nämlich jede Reizänderung nur relativ zu der schon vorhandenen Reizstärke und nicht absolut: das ist doppelt so hell, doppelt so laut, halb so laut oder der Ton ist doppelt so hoch wie ein anderer (eine Oktave). Mathematisch ergibt sich daraus ein Logarithmen-Gesetz. Man setzt beide Größen (z. B. die beiden zu vergleichenden Schallintensitäten I1 und I2, jeweils in W/m²) ins Verhältnis, logarithmiert dann: L = lg (I1/I2) und gibt diese Größe in Bel an (nach Graham Bell, dem Erfinder des Telefons). Der Intensitätsunterschied, den ein Guthörender gerade wahrnehmen kann, beträgt etwa 0,1 Bel. Nun ist vor vielen Jahren ein „ganz Schlauer“ auf die Idee gekommen (damals waren die Schallpegelmesser in ihrer Anzeige noch nicht sehr genau) und hat 1 Bel in 10 dezi-Bel unterteilt. So wie 0,1 m = 1 dm ist, ist eben auch 0,1 B = 1 dB. Das hatte damals den Vorteil, dass man immer mit ganzen Zahlen ohne Nachkommastellen rechnen konnte. Moderne Schallpegelmesser sind so genau, dass sie 1/100 dB anzeigen können, was dann 1 mB (milli-Bel) entspricht.
Weil das Rechnen mit Logarithmen nicht jedermanns Sache ist, enthält die folgende Tabelle eine Aufstellung für die "glatten" Werte:
|
dezi-Bel |
Bel |
Intensitätsverhältnis |
|
|
0 |
0 |
10 0 |
1 : 1 |
|
10 |
1 |
10 1 |
1 : 10 |
|
20 |
2 |
10 2 |
1 : 100 |
|
30 |
3 |
10 3 |
1 : 1 000 |
|
40 |
4 |
10 4 |
1 : 10 000 |
|
50 |
5 |
10 5 |
1 : 100 000 |
|
60 |
6 |
10 6 |
1 : 1 000 000 |
|
70 |
7 |
10 7 |
1 : 10 000 000 |
Man sieht hier, dass das Intensitätsverhältnis gleich dem 10-hoch-Bel-Wert ist. In der folgenden Tabelle sind einige markante Werte angegeben und zwischen 50 und 60 dB noch einige „krumme“ Werte eingefügt. Daraus kann man z. B. erkennen, dass ein Schwerhörender mit einem Hörverlust von z. B. 55 dB erst dann ein Signal gerade eben wahrnimmt, wenn die (physikalisch messbare) Schallintensität 300 000 mal größer ist als bei der Hörschwelle guthörender Personen.
|
dezi-Bel |
Bel |
Intensitätsverhältnis |
|
|
0 |
0 |
10 0 |
1 : 1 |
|
3 |
0,3 |
10 0,3 |
1 : 2 |
|
5 |
0,5 |
10 0,5 |
1 : 3 |
|
7 |
0,7 |
10 0,7 |
1 : 5 |
|
40 |
4 |
10 4,0 |
1 : 10 000 |
|
43 |
4,3 |
10 4,3 |
1 : 20 000 |
|
45 |
4,5 |
10 4,5 |
1 : 30 000 |
|
47 |
4,7 |
10 4,7 |
1 : 50 000 |
|
50 |
5 |
10 5 |
1 : 100 000 |
|
53 |
5,3 |
10 5,3 |
1 : 200 000 |
|
55 |
5,5 |
10 5,5 |
1 : 300 000 |
|
57 |
5,7 |
10 5,7 |
1 : 500 000 |
|
60 |
6 |
10 6 |
1 : 1 000 000 |
Schallpegel ist nicht Lautstärke
Das subjektive Lautstärkeempfinden folgt nicht diesen physikalischen Gesetzen. Wenn ein um 3 dB höherer Schallpegel bedeutet, dass die Schallintensität dieses Signals doppelt so groß ist (siehe oben) wie die des Vergleichs-Signals, dann heißt das noch lange nicht, dass man dieses Signal auch als doppelt so laut empfindet. Guthörende Personen empfinden eine doppelte Lautstärke erst dann, wenn der Schallpegelunterschied zwischen den beiden Signalen etwa 10 dB beträgt. Genau genommen muss man sagen, dass verschiedene Testpersonen 8...12 dB Pegelunterschied etwa als Lautstärkeverdoppelung oder -halbierung empfinden. Die Hörversuche, an denen seinerzeit etwa 70 „normalhörende“ (ohrgesunde) Studenten unter 25 Jahren teilnahmen, haben aber im statistischen Mittel den Wert von 10 dB für die Verdoppelung oder Halbierung ergeben. Auch bei den Hörversuchen ist also jede Person ein Individuum.

Zwicker und Feldtkeller [4] haben in den 60er Jahren bei den oben erwähnten Untersuchungen festgestellt, dass oberhalb von etwa 40 dB jede Schallpegelzunahme um 10 dB von guthörenden Personen im Mittel etwa als Lautstärkeverdoppelung empfunden wird. Sie haben deshalb willkürlich 40 dB zu 1 sone (von sonare = tönen) gesetzt, 50 dB zu 2 sone, 60 dB zu 4 sone, 70 dB zu 8 sone usw.. An diesen Zahlenwerten kann man gut die Verdoppelung der „Lautheit“ erkennen. Zwicker und Feldtkeller haben ausdrücklich „Lautheit“ geschrieben, weil „Lautstärke“ oft mit „Schallpegel“ gleichgesetzt wird. Aus dieser Untersuchung resultiert die Aussage: 3 dB mehr sind zwar physikalisch doppelte Intensität, erst 10 dB mehr sind aber subjektiv etwa die doppelte Lautheit.
Für diejenigen, die es noch ein wenig genauer wissen wollen, kommt jetzt etwas Mathematik (aber nur ganz wenig): Nimmt man an, die eine Intensität sei doppelt so groß wie eine andere, es sei also A = 2B, dann kann man rechnen:
DL = 10 lg (A/B) = 10 lg (2B/B) = 10 lg 2 = 10 x 0,3010... dB ≈ 3 dB
Das heißt also, dass ein Intensitätsverhältnis von 2:1 einem Pegelunterschied von 3 dB entspricht (und der Kehrwert 1:2 = 1/2 entspricht -3 dB). Physikalisch betrachtet ist 3 dB mehr oder weniger also immer doppelt oder halb so viel. Beim subjektiven Lautstärkeempfinden gilt das nur für sehr niedrige Pegel, bei hohen Pegeln wird das Ohr - wie oben beschrieben - unempfindlicher.
Lärm ruft zu den Waffen: ALARM
Unterhalb von 40 dB stimmt bei guthörenden Personen die Aussage, eine Pegelveränderung um 10 dB sei halb/doppelt so laut, aber nicht mehr. Bei niedrigen Pegeln unterscheidet das Gehör genauer: Bei 30 dB reichen 5 dB Unterschied für halb/doppelt so laut und bei 20 dB reichen sogar nur 3 dB Unterschied und schon empfinden Guthörende ein Signal als halb/doppelt so laut. Das war früher lebenswichtig, damit man frühzeitig die Feinde oder die wilden Tiere anschleichen hörte. Dieses Wachsam-Sein-Müssen (genau genommen: Horchsam-Sein-Müssen) ist auch der Grund, warum man das Ohr im Schlaf und auch in der Narkose nicht schließen kann, wohl aber die Augen. Das Wort „Lärm“ und das Wort „Alarm“ haben deshalb den gleichen Wortstamm, weil die Wache, wenn sie wachsam war, beim leisen Annähern des Feindes „Alarm“ schlug, also Lärm machte und damit die Kampfgenossen zu den Waffen (ital.: al arme) rief.
Lärm setzt noch heute Adrenalin (= Stresshormon) frei und weckt unbewusst die Kampfbereitschaft, so dass wir uns in Abwehrhaltung begeben. Unter Lärm-Stress steigt deshalb auch das Herzinfarkt-Risiko beträchtlich. Man vermutet, dass heute mehr Menschen an lärmbedingtem Herzinfarkt sterben als durch Lärm schwerhörend werden.
„Etwas lauter“ ist „sehr laut“: Recruitment
Bei guthörenden Personen liegt zwischen der Hörschwelle (definiert als Schallpegel 0 dB) und der Schmerzschwelle eine Spanne von etwa 120 dB. Diese zwölf 10-dB-Stufen bedeuten somit eine 12-fache Verdoppelung der Lautstärkeempfindung: 1 / 2 / 4 / 8 / 16 / 32 / 64... Wenn aber bei schwerhörenden Menschen (mit Schallempfindungs-Schwerhörigkeit, das sind über 90% der Schwerhörenden) nicht nur die Hörschwelle um z. B. 50 dB angehoben ist, sondern auch die Unbehaglichkeitsschwelle von 120 dB auf z. B. 100 dB absinkt, dann steht für den gesamten Lautstärke-Empfindungsbereich nur noch eine Spanne von 50 dB, nämlich 50 ... 100 dB zur Verfügung. Zwischen „ganz leise“ und „ganz laut“ wird die Empfindungskurve also viel steiler. Mediziner sprechen dann von „Recruitment“, zu Deutsch „Lautheitsausgleich“. Bei Personen mit Schallleitungs-Schwerhörigkeit (Mittelohr-Schwerhörigkeit, unter 10%) tritt dieser Effekt nicht auf.
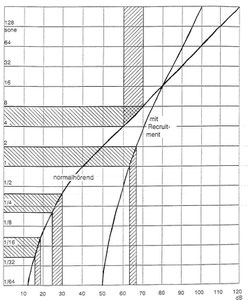
Schwerhörende empfinden deshalb auch kleine Schallpegel-Unterschiede häufig viel krasser, z. B. 2 oder 3 dB mehr sind dann doppelt so laut. Wenn ein Schwerhörender einen Guthörenden bittet etwas lauter zu reden, dann spricht der (nach seinem subjektiven Empfinden) etwa doppelt so laut, oder (physikalisch) mit einem 10 dB höheren Schallpegel. Für Menschen mit Recruitment sind das aber etwa 2 + 3 + 2 + 3 dB und damit rund 4 (!) Verdoppelungen. 1 / 2 / 4 / 8 / 16. Dann heißt es „Du brauchst doch nicht gleich zu schreien“ und beide haben Recht. Dieses Phänomen, bis zu einem gewissen Pegel (nämlich der individuellen Hörschwelle) gar nichts zu hören, oberhalb davon dann aber „wie ein Luchs“ hat zu vielen Anekdoten über Schwerhörende geführt. Weitaus ärgerlicher ist aber, dass die Aussage „ich höre doch noch gut, du brauchst gar nicht zu schreien“ dazu führt, dass die Betroffenen den Gehörschaden selbst viel zu spät (endlich) wahrnehmen.
Wichtiges ist hochfrequent
Es gibt noch ein weiteres Phänomen, das häufig im Gespräch über Schallpegel und Hörverluste vergessen wird: Das menschliche Gehör arbeitet nicht in allen Frequenzbereichen (also bei allen Tonhöhen) gleichartig, sondern sein Verhalten ist stark frequenzabhängig. Unser Ohr ist seit Jahrmillionen darauf eingerichtet, hohe Töne besonders gut zu hören: Das Gluckern von Wasser, das Rascheln von Laub und das Knacken von Ästen, auch das Surren einer Mücke. Mit solchen Geräuschen konnten sich Gefahren ankündigen. Wichtige Geräusche sind hochfrequent, z. B. auch die Klingel der Feuerwehr. Frauen haben hohe Stimmen, weil sie wichtigeres zu sagen haben und wir Männer haben dem nichts entgegen zu halten.
Auch die wichtigen Sprachanteile der Zisch- und Explosivlaute (im Wesentlichen die Konsonanten) liegen im hochfrequenten Bereich, während die Vokale mit starken tieffrequenten Komponenten nur die Lautstärke der Stimme ergeben: Bei Guthörenden reicht Flüstern für die vollständige Weitergabe von Informationen aus und das sind eben nur die hohen Frequenzen. Wenn man „M“ „TZ“ und „SCH“ spricht, so hört man schon wie das „M“ ein tieffrequentes Summen, das „SCH“ und noch mehr das „TZ“ ein hochfrequentes Zischen sind. Beide klingen wiederum deutlich unterschiedlich. Wenn man diesen unterschiedlichen Klang aber wegen eines Hörverlustes nicht mehr wahrnimmt, was dann? Dann wird eben aus „Mutter“ das Wort „Butter“ und aus „zu“ wird „Schuh“. Von den gut 35 Phonemen der deutschen Sprache lassen sich nur etwa 11 durch Absehen von den Lippen eindeutig erkennen, während man die anderen aus dem Zusammenhang heraus kombinieren muss, wenn man sie nicht mehr hören kann. Wie wichtig die Konsonanten sind, lässt sich grafisch gut veranschaulichen:
ie o o a e i i i e a ie o a e.
D K ns n nt n s nd w cht g r ls d e V k l .
Die Konsonanten sind wichtiger als die Vokale.
Nach meiner persönlichen Auffassung haben Frauen höhere Stimmen als Männer, weil sie auch Wichtigeres zu sagen haben. (Als Mann darf ich das behaupten.)
Wie hört man „normal“?
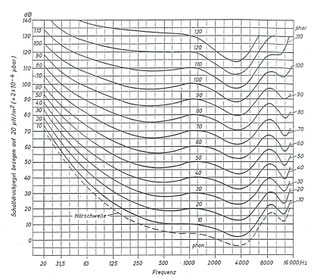
Die starke Frequenzabhängigkeit der Lautstärkeempfindung ist bei Guthörenden sehr genau untersucht. Bereits seit mehreren Jahrzehnten gibt es in einer DIN-Norm [3] die so genannten „Normalkurven gleicher Lautstärkepegel“. Deutlich ist zu erkennen, dass bei 1000 Hz der Schallpegel, der bei Guthörenden gerade eine Hörempfindung auslöst, willkürlich mit 0 dB festgelegt wurde. Das gilt für das Hören mit beiden Ohren; beim Hören mit einem Ohr braucht man wiederum 3 dB mehr Schallpegel. Auch hierbei handelt es sich wieder um den Mittelwert über eine große Anzahl von Testpersonen.
Es gibt also durchaus Menschen, die noch unter 0 dB etwas hören können. Sie hören buchstäblich „das Gras wachsen“, denn die Geräusche der „Brownschen Molekularbewegung“ der Luft liegen nur etwa 10 dB unter der Norm-Hörschwelle.
Zwischen 2000 und 4000 Hz sind durchgängig die Ohren aller Testpersonen etwas empfindsamer als bei 1000 Hz. In diesem Frequenzbereich ist das Ohr aber – wie viele Audiogramme zeigen – auch am empfindlichsten. Lärmschwerhörigkeit macht sich deshalb im Allgemeinen in diesem Frequenzbereich eher bemerkbar als bei noch höheren Tönen.
Man kann auch erkennen, dass die tiefen Töne offenbar recht unwichtig sind, denn sie müssen mit deutlich höheren Schallpegeln einwirken bis sie gleichlaut empfunden werden, wie hohe Töne. Hier hat sich offenbar das Ohr im Laufe mehrerer Millionen Jahre an die Wichtigkeit der uns umgebenden Geräuschwelt angepasst.
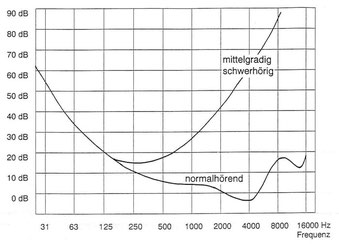
Die nebenstehende Abbildung enthält beispielhaft auch die Hörschwellenkurve eines mittelgradig Schwerhörenden. Die folgende Abbildung zeigt das zugehörige Audiogramm: Was rechts als Hörschwellenkurve „ziemlich verbogen“ aussieht, ist im Bild unten zu der „0-dB-Hörverlust-Geraden“ zurecht gerückt worden. In einem Audiogramm wird der Hörverlust – als Mangel – nach unten aufgetragen. Man benötigt für eine bestimmte Schallempfindung dann einen entsprechend der Hörschädigung höheren Schallpegel. Deshalb liegt in der Abbildung rechts die Hörschwellenkurve eines mittelgradig Schwerhörenden höher als die einer guthörenden Person.
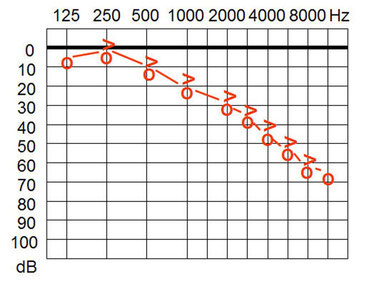
Während man aus dem Audiogramm entsprechend deutlich den jeweiligen Hörverlust erkennen und auch mit anderen Audiogrammen vergleichen kann (diese Darstellung bietet dem HNO-Arzt und dem Hörakustiker große Vorteile), kann man oben entnehmen, wie einschneidend die Veränderung in dem für das Sprachverständnis wichtigen hohen Frequenzbereich ist. Dabei ist dieser Vergleich insbesondere dann gut möglich, wenn nicht nur mit der Hörschwellenkurve, sondern auch mit den weiteren Kurven höherer Lautstärkeempfindungen verglichen wird.
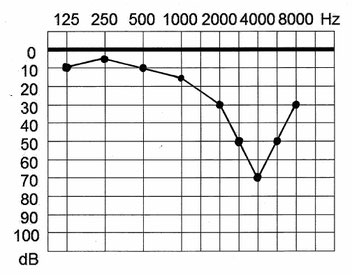
In dem Frequenzbereich, in dem unser Gehör besonders empfindam ist (etwa von 2000 Hz bis 5000 Hz), in dem ist es auch besonders empfindlich. Dort wird es also durch Lärm-Einwirkungen als erstes geschädigt. Das nebenstehende Tonaudiogramm zeigt beispielhaft die sogenannnte "c5-Senke" bei 4000 Hz. Dort liegt etwa der musikalische Ton des "fünfgestrichenen c", daher diese Bezeichnung.
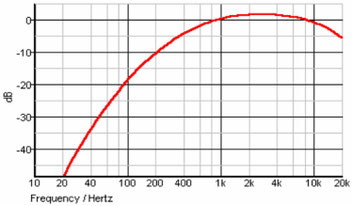
Das A-Filter: Versuch einer Annäherung
Um die Tonhöhenabhängigkeit der subjektiven Lautstärke-Empfindung von Guthörenden auch in die physikalische Angabe eines bestimmten Schallpegels mit einzubeziehen, hat man Filter in die Schallpegelmesser eingebaut, mit denen man das Signal bewertet, bevor es angezeigt wird. Eine beliebte Filterung (aber bei weitem nicht die beste) ist die „Bewertungskurve A“. Mit ihr wird eine Annäherung an die 40-Phon-Kurve versucht, um den physikalisch messbaren Schallpegel mit der subjektiv empfundenen Lautstärke näherungsweise zur Deckung zu bringen. So gemessene Schallpegel kennzeichnet man mit dB(A). Das Filter ist sehr einfach gehalten, weil man es bei seiner Entwicklung vor über 60 Jahren aus Widerständen und Kondensatoren herstellen musste. Es ermöglicht nur eine grobe Annäherung an das sehr komplexe Verhalten des menschlichen Gehörs. Man weiß damit, dass alle falsch messen, aber man ist sich auf diese Weise auch sicher, dass alle "gleich falsch" messen.
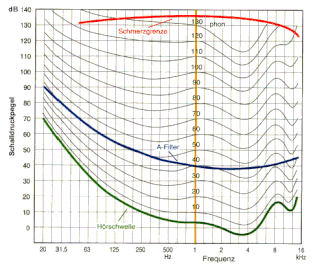
Wie schlecht diese Anpassung an die 40-Phon-Kurve ist, zeigt die nebnstehende Abbildung. Mit heutiger Digitaltechnik könnte man die Filter wesentlich genauer programmieren und somit eine bessere Anpassung an das subjektive Empfinden schaffen. Die dB(A)-Bewertung ist aber längst eine weltweit gängige Messmethode und in vielen Normen und Regelwerken sind Richt- oder Grenzwerte in dB(A) festgelegt. Eine bessere Messmethode würde deshalb nur an einer anderen Stelle zu erneuten Verunsicherungen führen. Generell verwendet man die Schallpegelangabe in dB(A) nur, wenn man die Einwirkung eines Gesamt-Schallereignisses auf den Menschen als „empfundene Lautstärke“ beschreiben (messen) will. Ein Hörverlust wird aber nicht in dB(A), sondern in dB beschrieben und man muss jeweils dazu angeben, bei welcher Frequenz dieser Wert gilt.
Exkurs: "Gehörschutz"
(Das gehört zwar nicht zu den Berechnungen, passt aber doch ganz gut hierher.)
Die Gesetze und Verordnungen zum Arbeitsschutz fordern, dass den Beschäftigten bei einem mittleren Schallpegel am Arbeitsplatz von 80 dB(A) persönliche Gehörschutzmittel zur Verfügung zu stellen sind und dass diese ab 85 dB(A) auch getragen werden müssen. Bei so hohen Schallpegeln verlaufen aber die "Kurven gleichen Lautstärkepegels" in dem obigen Diagramm deutlch flacher. Da ist die A-Bewertungskurve nur noch eine sehr schlechte Anpassung. Deshalb wurde für den Bereich des Gehörschutzes vor zu lauten Schallpegeln die C-Bewertungskurve genormt, die (ebenfalls nur grob) an die Kurven im Bereich zwischen 80 und 90 dB angepasst ist. Wenn also im Arbeitsschutz "ziemlich richtig" gemessen werden soll, dann ist am Schallpegelmesser die nicht die A-Bewertung, sondern die C-Bewertung einzuschalten.
Exkurs zum Exkurs (weil ich gerade mal dabei bin...)
Besonders gehörschädigend sind sehr kurze Schallimpulse, die unser Gehör als "gar nicht so laut" empfindet (hierzu zählen nicht nur die Schläge einer Dampframme sondern auch die vom Hammer eines Zimmermannes). Bei längeren lauten Geräuschen spannen sich die Muskeln im Mittelohr an und hindern Hammer, Amboß und Steigbügel daran, den ganzen Schall zum Innenohr durchzulassen. Diese Muskeln haben aber eine Reaktionszeit von etwa 35 ms. Impulse, die kürzer sind, haben "freie Fahrt". Deshalb misst man im Bereich des Gehörschutzes nicht mit der Zeitbewertung "fast", sondern richtigerweise mit "peak". Bei Schallpegeln mit LCPk > 130 dB können bereits einzelne Impulse das Gehör bleibend schädigen.
Mehr dazu gibt es in dem Abschnitt "Schallpegelmessungen einst und jetzt". Im Zusammenhang mit der geschichtlichen Entwicklung kann man vielleicht besser verstehen, warum man bestimmte Dinge heute so handhabt und nicht "viel besser und richtiger".
Was gilt denn nun?
Während man bei Guthörenden recht genau angeben kann, welche Schallpegelunterschiede mit welchen Lautheitsunterschieden korrelieren, ist dies bei Schwerhörenden nicht möglich. So wenig wie es eine mittlere Schwerhörigkeit gibt, so wenig gibt es auch ein mittleres Empfinden. Bei Guthörenden ist die Abhängigkeit vom Schallpegelunterschied, von der absoluten Höhe des Schallpegels und von der Frequenz (= Tonhöhe) recht genau bekannt. Bei Schwerhörenden kommen noch die Abhängigkeit vom Hörverlust (der seinerseits bei verschiedenen Frequenzen unterschiedlich ist) und von der Steilheit des Recruitment hinzu. Deshalb reagiert jede Person anders.
„We are still confused, but on a higher level.“
Exkurs: Wann Faktor 10 und wann Faktor 20?
Das menschliche Gehör kann nur eine Dynamik der Schalldrücke von 1 / 1.000.000 verarbeiten. Das sind doch nur sechs Dekaden, also 106 oder 60 dB. Wieso reichen dann die Schallpegel von 0 dB bis 120 dB?
Hier beschreibe ich etwas, das ich während meines Akustik-Studiums bis zum Diplom nicht verstanden habe. Erst viel später habe ich es gelernt und begriffen. Und wenn ich es heute erläutern will, dann winken die meisten Leute wegen des Rechnens mit Logarithmen ab und verstehen es dann lieber doch nicht. Aber ich probiere es jetzt mal:
Das Mikrofon am Schallpegelmesser misst den Schalldruck. Deshalb heißt die genaue Bezeichnung auch Schalldruckpegel. Das Rechnen mit Schalldrücken ist aber physikalisch deshalb nicht korrekt, weil es eigentlich überall um Schallleistungen geht. In der Schallleistung steckt aber der Schalldruck quadratisch. Das ist vergleichbar mit der elektrischen Leistung, die quadratisch von der Spannung abhängt (oder quadratisch vom Strom, je nachdem, wie man das Ohm’sche Gesetz anwendet). Um noch weiter zu verwirren: die Schallintensität ist ebenfalls eine Leistungs-Größe. Sie ist nämlich diejenige Schallleistung, welche durch eine gedachte Fläche von 1 m² hindurch tritt. Das ist aber nur dann interessant, wenn man die Schallleistung einer Quelle messtechnisch ermitteln will. Dann legt man nämlich eine gedachte Messfläche um diese Schallquelle und die wird eben in Quadratmeter gemessen. Geht man doppelt so weit von der Schallquelle weg, dann ist dort die Hüllfläche viermal so groß. Auch da steckt also wieder die quadratische Abhängigkeit drin.
Jetzt geht es richtig los mit der Mathematik:
Der Schalldruckpegel ist also eigentlich der Pegel
der Schalldruck-Quadrate: Lp = 10 lg (p²/p0²) dB
der Schallleistungen: LW = 10 lg (P/P0) dB
der Schallintensitäten: LI = 10 lg (I/I0) dB
Diese Gleichungen sehen alle identisch aus, aber nur deshalb, weil beim Schalldruckpegel der Logarithmus einer quadratischen Größe gebildet wird. Dadurch, dass man den aktuellen Wert immer durch einen Bezugswert (p0, P0 oder I0) dividiert, steht unter dem Logarithmus eine reelle Zahl ohne Einheit, weil die sich weg-kürzt. (Und weil der mit 10 multiplizierte Logarithmus einer reellen Zahl wieder eine reelle Zahl ist, ist das dB auch keine „Einheit“, sondern nur die „Kennzeichnung“, dass es sich hier um ein „logarithmiertes Größenverhältnis“ handelt.)
Man kann den Schalldruckpegel aber auch wie folgt schreiben:
Lp = 10 lg (p²/p0²) dB = 20 lg (p/p0) dB
Wenn das Argument eines Logarithmus quadratisch ist, dann kann man das Quadrat auch vor den Logarithmus ziehen, indem man dort mit 2 multipliziert. Nichts anderes ist bei dieser Schreibweise passiert.
Die Aussage, unser Ohr könne Schalldrücke von 1 / 1.000.000 verarbeiten, kann man auch wie folgt schreiben:
Lp = 20 lg (1.000.000/1) dB = 20 lg (106/1) dB = 120 dB oder
Lp = 10 lg (1.000.000²/1²) dB = 10 lg
((106)2/1) dB = 10 lg (1012/1)
= 10 lg (1.000.000.000.000/1) dB = 120 dB
Die beiden Lesarten sind also identisch, denn die Billion ist das Quadrat der Million, 1² ist aber wieder 1.
Auch bei den Verdoppelungen der Lautstärke, des Schalldruckpegels und der Schall-Leistung stehen immer wieder die Aussagen 3 dB oder 6 dB nebeneinander (oder gegeneinander).
Wenn man den Schalldruck verdoppelt, dann vervierfacht man damit die Schallleistung:
∆L = 10 lg (2²/1²) = 10 lg (4/1) = 20 lg (2/1) = 6 dB
Wenn man aber die Schallleistung (nur) verdoppelt, dann gilt
∆L = 10 lg (2/1) = 3 dB.
Mathematik kann man nicht lernen, aber man kann sich daran gewöhnen!
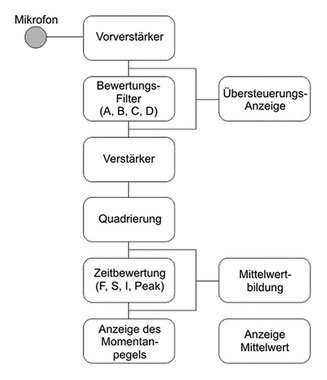
In der "Städtebaulichen Lärmfibel" des Landes Baden-Württemberg habe ich im Kapitel 2.4.4.3 "Messgeräte" als Abb.
2.12 das Blockschaltbild eines Schallpegelmessers gefunden. Dort ist die "Quadrierung" als eigenständiges Bauteil abgebildet.
Damit wird das Signal gleichzeitig auch gleichgerichtet und es gibt nur noch positive Spannungen (+*+ = + und -*- = +). Sonst würde das Drehspulinstrument im Messgerät infolge der Trägheit als
Mittelwert der positiven und negativen Halbwellen immer nur "0" anzeigen.
Aus diesem Blockschaltbild ist also gut erkennbar, dass die gemessenen Schallpegel mit genauer Bezeichnung SchallDRUCKpegel sind und schließlich mit ganz genauer Bezeichnung SchalldruckQUADRATpegel. Das sagt aber leider niemand und deshalb gibt es für diejenigen, die Schallmessungen nur "im Nebenfach" machen immer wieder Verwirrungen. Auch mir ist das seinerzeit so gegangen, denn selbst mein Assi in der Uni konnte das nicht erklären. Vielleicht hatte er selbst es ja auch noch nicht verinnerlicht, weil niemand es ihm erklären konnte?
ACHTUNG: Nach meiner Auffassung ist auch dieses Blockschaltbild nicht ganz richtig, denn die Übersteuerungsanzeige darf die Filter nicht überbrücken (und damit unwirksam machen) und die Mittelwertbildung kommt erst NACH der Zeitbewertung und nicht parallel.
[1] Weber, Ernst Heinrich: Die Lehre vom Tastsinn und Gemeingefühl, Braunschweig. 1851
[2] Fechner, Gustav Theodor: Elemente der Psychophysik, Breitkopf und Härtel, Leipzig, 1860
[3] DIN ISO 226:2006-04: Normalkurven gleicher Lautstärkepegel
[4] Zwicker, Eberhard und Feldtkeller, Richard: Das Ohr als Nachrichtenempfänger, Hirzel-Verlag, Stuttgart, 1967
Wer jetzt noch Zeit und Lust hat, kann gleich noch Kopfrechnen üben...
Anschrift:
Rethwisch 10
25497 Prisdorf
Kontakt:
Tel.: 04101 79 37 56
Mail: post(@)carsten-ruhe(.)de
Öffnungszeiten:
von Montag bis Sonntag
von 08:00 bis 22:00
Steuer-Nummer:
UStID.: DE134438564
